niusouti.com

高斯用尺规作图绘出了正17边形，为欧几里得几何提供了重要的补充。

题目

高斯用尺规作图绘出了正17边形，为欧几里得几何提供了重要的补充。

相似考题

1.高斯被称为数学王子,他在19岁时就做解决了一个重要的作图问题,这个问题是使用尺规解决了立方倍积问题。()此题为判断题(对，错)。

2.在( )中,那速?拉丁指出了由球面三角形的三个角可以求出三边或由三边去求三个角。 此事实可以作平面三角与球面三角差异的重要标志。A.《论四边形》B. 《代数学》C. 《几何作图法》D. 《星的科学》

3.古典几何三大尺规作图问题是()?A.三等分任意角B.化圆为方C.正多边形D.倍立方体

4.高斯被称为数学王子,他在19岁时就做解决了一个重要的作图问题,这个问题是:()A.使用尺规进行三等分角B.使用尺规解决了立方倍积问题C.使用尺规解决了化圆成方问题D.使用尺规做出了正十七边形

更多“高斯用尺规作图绘出了正17边形，为欧几里得几何提供了重要的补充。”相关问题

  • 第1题：

    欧几里得几何原本的陈述有它的不足之处,到了十九世纪由()提出了一个完善的欧几里得几何公理系统,并由此解决了用公理方法研究几何学的基础问题。

    A、希尔伯特

    B、罗巴切夫斯基

    C、帕斯卡

    D、傅立叶


    正确答案:A

  • 第2题：

    简述“尺规作图”的基本要求，并写出古希腊时期“几何作图三大问题”的具体内容。


    答案：
    解析：
    本题主要考查有关“尺规作图”，以及“几何作图三大问题” 的相关数学史知识。

    尺规作图是指用没有刻度的直尺和圆规作图。①尺规作图使用的直尺和圆规带有想象性质，跟现实中的并非完全相同；②直尺必须没有刻度，无限长，且只能使用直尺的固定一侧。只可以用它来将两个点连在一起，不可以在上画刻度；③圆规可以开至无限宽，但上面亦不能有刻度。它只可以拉开成之前构造过的长度。

    尺规作图是起源于古希腊的数学课题。只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题。①三等分角问题：三等分一个任意角；②倍立方问题：作一个立方体，使它的体积是已知立方体的体积的两倍；③化圆为方问题：作一个正方形，使它的面积等于已知圆的面积。

    以上三个问题在2400年前的古希腊已提出这些问题，但在欧几里得几何学的限制下，以上三个问题都不可能解决的。直至1837年，法国数学家万芝尔才首先证明“三等分角”和“倍立方”为尺规作图不能问题。而后在1882年德国数学家林德曼证明π是超越数后，“化圆为方”也被证明为尺规作图不能问题。

  • 第3题：

    古希腊的三大闻名几何尺规作图问题是()。
    ①三等分角②立方倍积③正十七逸形④化圆为方

    A.①②③
    B.①②④
    C.①③③
    D.②③④。

    答案：B
    解析：
    大约在公元前6世纪至4世纪之间，古希腊人遇到了令他们百思不得其解的三大尺规作图问题，这就是著名的古代几何作图三大难题：(1)三等分角问题：将任一个给定的角三等分；(2)立方倍积问题：求作一个正方体的棱长，使这个正方体的体积是已知正方体体积的二倍；(3)化圆为方问题：求作一个正方形，使它的面积和已知圆的面积相等。@##

  • 第4题：

    已知一个圆O，用钢板尺、划规、划针作圆O的内接正七边形。

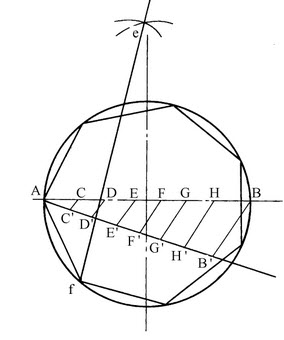
    （1）在圆O内作直径AB，把AB分成7等份得C、D、E、F、G、H点。
    （2）分别以A、B为圆心，AB长为半径作弧交于e点。
    （3）连接eD，并延长交圆周于f。
    （4）用Af长等分圆周，连接各分点即成所作圆O的内接正七边形。
    略

  • 第5题：

    （）关于歌尼斯堡七桥问题和关于多面体顶点、边和面关系的讨论，是几何学发展的重要突破，此时关心的不再是度量问题，而是位置问题、连接问题。

    • A、欧几里得
    • B、欧拉
    • C、海亚姆
    • D、高斯

    正确答案:B

  • 第6题：

    日本人利用（）的方法计算出了粗略的球的体积。

    • A、组合
    • B、尺规作图
    • C、假设法
    • D、切片

    正确答案:D

  • 第7题：

    在黄金分割的尺规作图中，画出了几个圆心（）

    • A、0
    • B、1.0
    • C、2.0
    • D、3.0

    正确答案:C

  • 第8题：

    作图题：在已知圆内作内接正六边形。


    正确答案: 过已知圆的圆心O，作直径ab、以a、b点为圆心，oa和ob为半径画弧与已知圆相交于c、d和e、f点依次连接ac、ce、eb、bf、fd、da该六边形即为圆的内接六边形。

  • 第9题：

    单选题
    《几何原本》是欧洲数学的基础，其作者是（  ）。
    A

    欧几里得

    B

    毕达哥拉斯

    C

    高斯

    D

    阿基米德


    正确答案： C
    解析：

  • 第10题：

    单选题
    《几何基础》的作者是（）
    A

    高斯

    B

    罗巴契夫斯基

    C

    希尔伯特

    D

    欧几里得


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    在黄金分割的尺规作图中，画出了几个圆心（）
    A

    0

    B

    1.0

    C

    2.0

    D

    3.0


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    哪种正多边形可以尺规作图？（）
    A

     正五边形

    B

     正十七边形


    正确答案： A
    解析： 暂无解析

  • 第13题：

    蜂窝式组网将一个移动通信服务区划分成许多以()为基本几何图形的覆盖区域，称为蜂窝小区。

    A、正六边形

    B、正五边形

    C、正四边形

    D、正八边形


    参考答案：A

  • 第14题：

    古希腊的三大著名几何尺规作图问题是()。
    ①三等分角②立方倍积③正十七边形④化圆为方


    A.①②③

    B.①②④

    C.①③④

    D.②③④

    答案：B
    解析：
    大约在公元前6世纪至公元前4世纪之间，古希腊人遇到了令他们百思不得其解的三大尺规作图问题，这就是著名的古代几何作图三大难题：(1)三等分角问题：将任一个给定的角三等分；(2)立方倍积问题：求作一个正方体的棱长，使这个正方体的体积是已知正方体体积的二倍；(3)化圆为方问题：求作一个正方形。使它的面积和已知圆的面积相等。

  • 第15题：

    许多几何学用语，如“点、线、面、三角形、四边形”等均出自《几何原本》一书，该书的作者为（　　）。

    A.祖冲之
    B.欧几里得
    C.伽利略
    D.阿基米德

    答案：B
    解析：
    《几何原本》是古希腊数学家欧几里得所著的一部数学著作，共十三卷。它是现代数学的基础，在西方是仅次于《圣经》的流传最广的书籍。

  • 第16题：

    用划规、划针、钢板尺作边长为30mm的正四方形，并写出作图步骤。
    见图E－32所示。

    （1）作线段AB＝30mm。
    （2）R＝30mm，R1＝＝42.426mm。 （3）以A为圆心，以R＝30mm为半径作弧，以B点为圆心，以R1＝42.426mm为半径作弧，两弧交于D点。
    （4）以B为圆心，以R＝300mm为半径作弧，以A为圆心，以R1＝42.426mm为半径作弧，两弧交于C点。
    （5）连接AD、DC、CB，作为ABCD正四方形。
    略

  • 第17题：

    高斯被称为数学王子，他在19岁时就做解决了一个重要的作图问题，这个问题是：（）。

    • A、使用尺规进行三等分角
    • B、使用尺规解决了立方倍积问题
    • C、使用尺规解决了化圆成方问题
    • D、使用尺规做出了正十七边形

    正确答案:D

  • 第18题：

    《几何基础》的作者是（）

    • A、高斯
    • B、罗巴契夫斯基
    • C、希尔伯特
    • D、欧几里得

    正确答案:C

  • 第19题：

    古希腊的三大闻名几何尺规作图问题是（）.①三等分角②立方倍积③正十七边形④化圆为方

    • A、①②③
    • B、①②④
    • C、①③④
    • D、②③④

    正确答案:B

  • 第20题：

    单选题
    （）关于歌尼斯堡七桥问题和关于多面体顶点、边和面关系的讨论，是几何学发展的重要突破，此时关心的不再是度量问题，而是位置问题、连接问题。
    A

    欧几里得

    B

    欧拉

    C

    海亚姆

    D

    高斯


    正确答案： C
    解析： 欧拉1736年关于歌尼斯堡七桥问题和1752年关于多面体顶点、边和面关心的讨论，是几何学发展的重要突破，此时关系的不再是度量问题，而是位置问题、连接问题。

  • 第21题：

    单选题
    古希腊的三大闻名几何尺规作图问题是（）.①三等分角②立方倍积③正十七边形④化圆为方
    A

    ①②③

    B

    ①②④

    C

    ①③④

    D

    ②③④


    正确答案： C
    解析： 暂无解析

  • 第22题：

    判断题
    高斯用尺规作图绘出了正17边形，为欧几里得几何提供了重要的补充。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第23题：

    单选题
    许多几何学用语，如“点、线、面、三角形、四边形”等均出自《几何原本》一书，该书的作者为（）。
    A

    祖冲之

    B

    欧几里得

    C

    伽利略

    D

    阿基米德


    正确答案： A
    解析： 《几何原本》是古希腊数学家欧几里得所著的一部数学著作，共十三卷。它是现代数学的基础，在西方是仅次于《圣经》的流传最广的书籍。

相关内容