如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8, AB∥DE,求△DEC的周长。
题目
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8, AB∥DE,求△DEC的周长。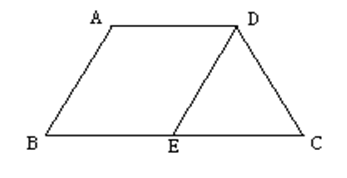

相似考题
更多“如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8, AB∥DE,求△DEC的周长。”相关问题
-
第1题:
如图.已知圆⊙O是△ABC的外接圆,AD是圆⊙0的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB。
(1)求证:BE是⊙0的切线;
(2)若BC=√3,AC=5,求圆的直径AD及切线BE的长。答案:解析:(1)连接OB,∵AD是圆⊙O的直径'∴∠OBD+∠EBD=90°, ∵BD=BC,∴其劣弧所对的圆周角相等,即∠CAB=∠BAD,
∵AO=BO,∴∠BAD=∠ABO,
又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°,
∵B0是圆的半径,∴BE是⊙O的切线。
(2)设圆的半径为r,连接CD交OB于F,
设圆的半径为R,连接CD,.
-
第2题:
如右图,在直角梯形ABCD中,AB,∥CD,AD⊥CD,AB=1cm,AD=6cm,CD=9cm,则BC=________cm.
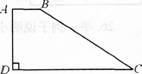 答案:解析:
答案:解析:
-
第3题:
如图,面积为20的正方形ABCD中,有一个小正方形EFGH,其中E,F,G分别在AB,BC,FD上,若BF=√5/2,则小正方形的周长是()。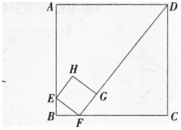 A.5√5/8
A.5√5/8
B.5√5/6
C.5√5/2
D.10√5/3答案:C解析: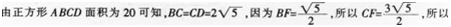

-
第4题:
如图所示,梯形ABCD,AD∥BC,DE⊥BC,现在假设AD、BC的长度都减少10%,DE的长度增加10%,则新梯形的面积与原梯形的面积相比,会怎样变化?
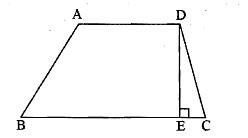
A. 不变
B. 减少1%
C. 增加10%
D. 减少10%答案:B解析:解题指导: S=90%(AD+BC)*100%DE÷2=99(AD+BC)*DE÷2,所以减少了1%。故答案为B。 -
第5题:
在三角形ABC,AB=4,AC=6,BC=8,D为BC的中点,则AD=
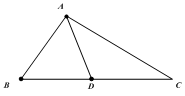
 答案:B解析:
答案:B解析:
-
第6题:
如右图所示,梯形ABCD的对角线AC丄BD,其中AD=1/2,BC=3,AC=2,BD=2.1,则梯形ABCD的髙AE的值是()。
 答案:C解析:由ACXBD=(AD+BC)XAE=>AE=42/45。
答案:C解析:由ACXBD=(AD+BC)XAE=>AE=42/45。 -
第7题:
如图在ΔABC中,DE∥BC,若AD:DB=1:3,DE=2,则BC等于( )。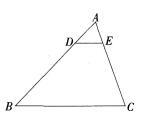 A.8
A.8
B.6
C.4
D.2答案:A解析:由于DE∥BC,所以DE:BC=AD:AB,又由AD:DB=1:3,所以AD:AB=1:4,由DE=2得BC=8。 -
第8题:
如图,在一张矩形纸片ABCD中,AB=4,BC=8。点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点日处,点D落在G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时, 。以上结论中,你认为正确的有( )个。 A.1
A.1
B.2
C.3
D.4答案:C解析:
-
第9题:
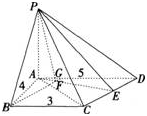
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90o,E是CD的中点。
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积。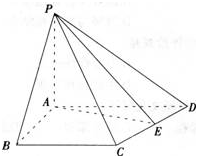 答案:解析:
答案:解析:
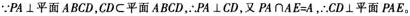

-
第10题:
铰链四杆机构ABCD中,已知AB=25mm、BC=70mm、CD=65mm、AD=95mm,当AD为机架时,是()机构,当AB为机架时,是()机构。
正确答案:曲柄摇杆;双曲柄 -
第11题:
铰链四杆机构ABCD,如果以BC为机架(静件),当机构为双曲柄机构时,各杆的长度可为()。
- A、AB=130 BC=150 CD=175 AD=200
- B、AB=150 BC=130 CD=165 AD=200
- C、AB=175 BC=130 CD=185 AD=200
- D、AB=200 BC=150 CD=165 AD=130
正确答案:C -
第12题:
单选题临床分期属( )。AⅢA
BⅢB
CⅣA
DⅣB
EⅡB
正确答案: E解析: 暂无解析 -
第13题:
在平行四边形ABCD中,∠DAB=60,AB=15cm,已知圆O的半径等于3cm,AB,AD分别与圆O相切于点E,F.圆0在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止.试求圆O滚过的路程.答案:解析:
-
第14题:
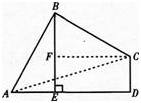
如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.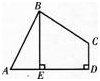
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.答案:解析: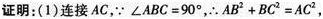
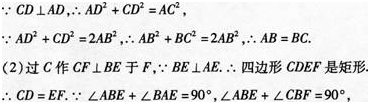

-
第15题:
如图,平面四边形ABCD中,AB=2,BC=4,CD=5,DA=3,
(1)若∠B与∠D互补,求AC2的值;
(2)求平面四边形ABCD面积的最大值。 答案:解析:
答案:解析: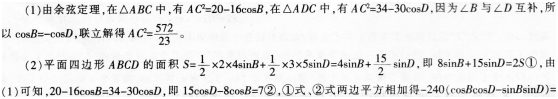
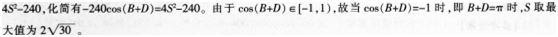
-
第16题:
如图所示,梯形ABCD的两条对角线AD、BC相交于O,EF平行于两条边且过O点。现已知AB=6,CD=18。问EF的长度为多少?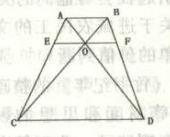 A. 8.5
A. 8.5
B. 9
C. 9.5
D. 10答案:B解析:解题指导: 18*BF/BD=6*DF/BD, BF/DF=1:3, OF/CD=1:4, OE/CD=1:4, EF=CD/2=9,故答案为B。 -
第17题:
如图6-9所示,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为( )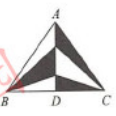 A.3
A.3
B.7.5
C.15
D.30
E.5.5答案:B解析:
-
第18题:
如图,已知四棱锥P-ABCD底面ABCD为矩形,侧棱PA⊥ABCD,AB=AP=21/2AD=2,E,F分别为PC,AB的中点。
(I)证明:EF∥面PAD。
(II)求三棱锥B-PFC的体积。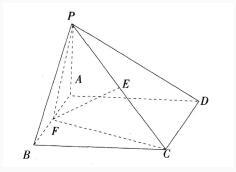 答案:解析:
答案:解析:
-
第19题:
如图,平行四边形ABCD,∠ADC的角平分线DE交BC于E,且AD=14,DC=9,
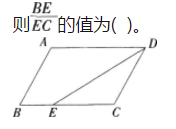
 答案:C解析:
答案:C解析:
-
第20题:
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P是BC边的中点,AD=2,SA=AB=1。

(1)求证:PD⊥平面SAP;
(2)求三棱锥S-APD的体积。答案:解析:(1)证明:易知在△APD中,,AD=2,满足勾股定理,故PD⊥AP。SA⊥底面ABCD,则SA⊥PD。PD同时垂直于平面SAP内的两条相交直线,PD⊥平面SAP。 (2)
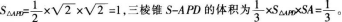
-
第21题:
存款冲销业务需()级主管授权。
- A、A
- B、B
- C、5万以上需A
- D、10万以上需A
正确答案:A -
第22题:
在铰链四杆机构ABCD中,已知AB=25mm,BC=70mm,CD=65mm,AD=95mm,当AD为机架时,是()机构;当AB为机架时,是()机构。
正确答案:曲柄摇杆机构;双曲柄机构 -
第23题:
在下列铰链四杆机构中,若以BC杆件为机架,则能形成双摇杆机构的是()。 (1)AB=70mm,BC=60mm,CD=80mm,AD=95mm (2)AB=80mm,BC=85mm,CD=70mm,AD=55mm (3)AB=70mm,BC=60mm,CD=80mm,AD=85mm (4)AB=70mm,BC=85mm,CD=80mm,AD=60mm
- A、(1)、(2)、(4)
- B、(2)、(3)、(4)
- C、(1)、(2)、(3)
正确答案:A
