已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为( )A.248 B.168 C.128 D.19 E.以上选项均不正确
题目
B.168
C.128
D.19
E.以上选项均不正确
相似考题
更多“已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为( )”相关问题
-
第1题:
一个等差数列,它的开始四项之和为70,最后四项之和为10,所有项的和为640,则这个数列一共有( )项。
A、 56 B、 60 C、 64 D、 72
因为前四项之和为40,最后四项之和为80 所以a1+an=(40+80)/4=30 Sn=n(a1+an)/2=30n/2=210 n=14
-
第2题:
若数列{xn}满足条件x1=3,xn+1=(x2n+1)/2xn ,则该数列的通项公式xn=____.
参考答案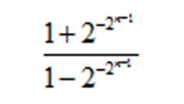
-
第3题:
设{an}与{bn}为两个数列,下列说法正确的是(). 答案:D解析:
答案:D解析:
-
第4题:
—个公比为2的等比数列,第n项与前n-1项和的差等于5,则此数列前4项之和为:A.70
B.85
C.80
D.75答案:D解析: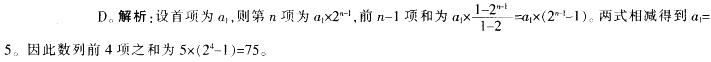
-
第5题:
已知等比数列{an}的各项都是正数,且a1+a3=10,a2+a3=6.
(I)求{an}的通项公式;
(II)求{an)的前5项和.答案:解析:
-
第6题:
已知数列{an}中,Sn是它的前n项和,并且Sn+1=4an+2,a1=1.
(Ⅰ)设bn=an+1-2an,求证:数列{bn)是等比数列;
(Ⅱ)设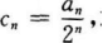 求证:数列{cn}是等差数列;
求证:数列{cn}是等差数列;
(Ⅲ)求数列{an}的通项公式及前n项和.答案:解析:
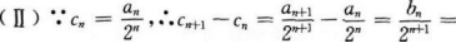


-
第7题:
已知数列{%}的前n项和是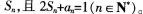
(1)求证:数列{an}是等比数列:
(2)记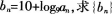 的前n项和Tn的最大值及相应的n值。 答案:解析:
的前n项和Tn的最大值及相应的n值。 答案:解析:
-
第8题:
(10分)等比数列{an}各项均为正数,且2a1+3a2=1,a32=9a2a6。
(1)求数列{an}通项公式;
(2)
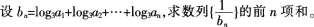 答案:解析:
答案:解析:
-
第9题:
已知数列{an}满足a1=2,an+1=3an+2(n∈N*),
(1)求数列{an}的通项公式;
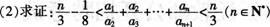 答案:解析:
答案:解析:

-
第10题:
已知数列{an}的前n项和是Sn,且2Sn+an=1(n∈N*)。
(1)求证:数列{an}是等比数列;
(2)记bn=10+log9an,求{bn}的前n项和Tn的最大值及相应的n值。答案:解析: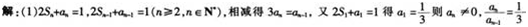
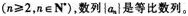
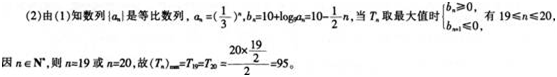
-
第11题:
单选题一个数列,前两项是1,从第三项开始,每一项都等于前两项之和,称为:()。A求和数列
B加和数列
C子空间数列
D斐波那契数列
正确答案: B解析: 暂无解析 -
第12题:
单选题“斐波那契数列”在求通项公式时,没有用到的知识是:()。A一元二次方程求根公式
B求极限
C等比数列通项公式
D二元一次方程组解法
正确答案: A解析: 暂无解析 -
第13题:
已知数列{an}的通项公式为an =(4 9) n-1 - (2 3) n-1 (n ∈ N∗ ),则数列{an}( ).
(A)有最大项,没有最小项.
(B)有最小项,没有最大项.
(C)既有最大项又有最小项.
(D)既没有最大项也没有最小项.
参考答案C -
第14题:
一个等差数列,它的开始四项之和为70,最后四项之和为10,所有项的和为640,则这个数列一共有( )项。
A、 56
B、 60
C、 64
D、 72
正确答案:C
C 解析:由等差数列的性质可知,等差数列的和为项数乘以平均数。本题中,由前四项和后四项的和,可求出平均数为(70+10)÷8=10,因此项数为 640÷10=64。故本题正确答案为C。 -
第15题:
一个公比为2的等比数列,第n项与前n-1项和的差等于3,则此数列的前4项之和为:
A.54
B.45
C.42
D.36答案:B解析:设首项为a1,则第n项为a1×2 n-1,前n-1项和为 两式相减得到a1 =3,因此数列前四项之和为3×(24-1)=45.
两式相减得到a1 =3,因此数列前四项之和为3×(24-1)=45. -
第16题:
已知等差数列前n项和
(Ⅰ)求这个数列的逋项公式;
(II)求数列第六项到第十项的和.答案:解析: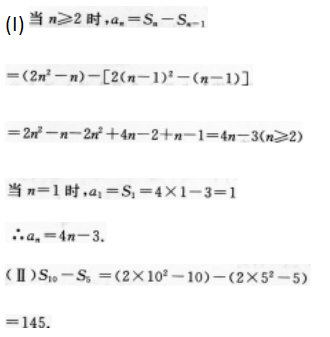
-
第17题:
已知等比数列{an}的各项都是正数,且a1+a3=10,a2+a3=6.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求{an}的前5项和.答案:解析:解:(Ⅰ)设(an)的公比为q,由已知得
-
第18题:
已知数列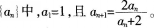 (1)求证:数列
(1)求证:数列 是等差数列:
是等差数列:
(2)求数列 的通项公式。 答案:解析:
的通项公式。 答案:解析: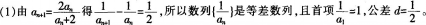 (2)数列
(2)数列 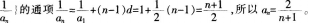
-
第19题:
一个等差数列首项为32,该数列从第15项开始小于1,则此数列的公差d的取值范围是().?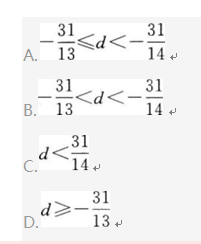 答案:A解析:
答案:A解析: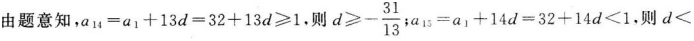
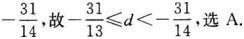
-
第20题:
(10分)已知数列{an}满足a1=3,an+1= an +2n,
(1)求{ an }的通项公式an;
(2)若bn=n an,求数列{bn}的前n项和sn。答案:解析:
-
第21题:
(10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数):
(1)求数列{ an }的通项公式;(4分)
(2)若a1=2,求数列{n an }的前n项和Tn。(6分)答案:解析:
-
第22题:
在移动平均中,设移动n年则()。
- A、当n为偶数时,移动后所得新数列较原数列首尾各缺n∕2项
- B、当n为奇数时,移动后所得新数列较原数列首尾缺(N-1)∕2项
- C、当n为偶数时,移动后所得新数列较原数列首尾缺n项
- D、当n为奇数时,移动后所得新数列较原数列首尾缺n项
正确答案:A,B -
第23题:
单选题数列“bn=b1nqn-1”为:()。A等差数列
B常数列
C等比数列
D无法确定
正确答案: D解析: 暂无解析
